BTC セクション3
ブロック構造と暗号技術
― ビットコインは「なぜ改ざんできない」のか?
ビットコインの強さは「分散しているから」だけではありません。
その本質は、ブロック構造と暗号技術が密接に組み合わさった設計にあります。
このセクションでは、
- ブロックとは何でできているのか
- なぜ過去の取引を変更できないのか
- 暗号技術がどこで、どのように使われているのか
を、設計思想ベースで解説します。
1. ブロックとは何か?
― ビットコインの「記録単位」
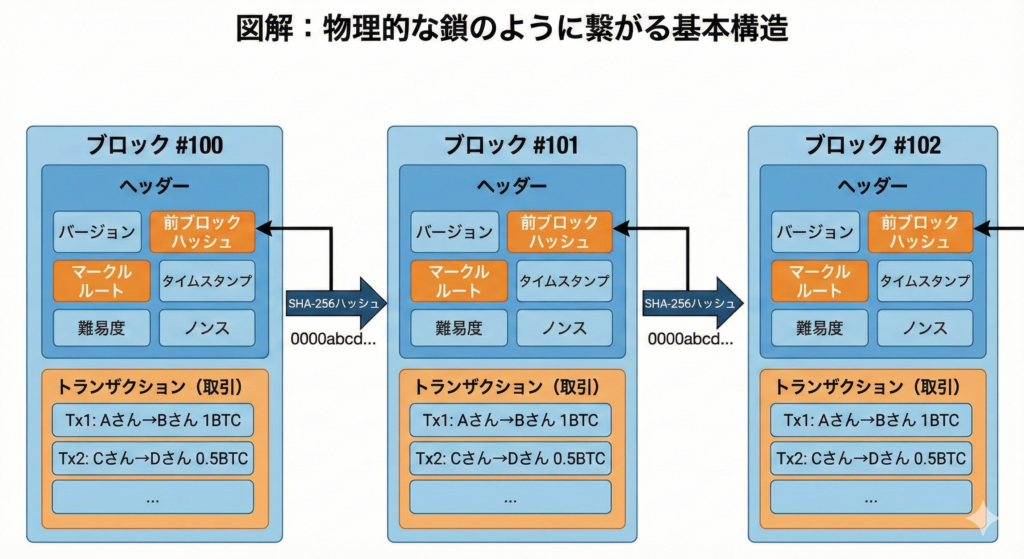
ビットコインの台帳は「ブロック」と呼ばれる単位で管理されています。
1つのブロックには以下が含まれます。
- 複数のトランザクション(取引)
- そのブロック自体の情報(ブロックヘッダー)
ブロックは約10分ごとに生成され、
過去のブロックに鎖(チェーン)のようにつながっていくことで
ブロックチェーンが形成されます。
2. ブロックの中身:ブロックヘッダーの正体
実は、ブロックの核心は「取引データ」そのものではなく、
80バイトのブロックヘッダーにあります。
ブロックヘッダーの主な要素
| 項目 | 役割 |
|---|---|
| バージョン | 使用しているプロトコル |
| 前ブロックのハッシュ | ブロック同士を鎖でつなぐ |
| マークルルート | ブロック内全取引の要約 |
| タイムスタンプ | 作成時刻 |
| 難易度ターゲット | PoWの条件 |
| ノンス | マイニングで探索される値 |
ここで重要なのは、
「前のブロックのハッシュ」が必ず含まれているという点です。
3. ハッシュ関数:改ざん検知の中核技術
ビットコインでは SHA-256 というハッシュ関数が使われています。
ハッシュ関数の特徴
- 入力が1ビットでも変わると、出力は完全に変わる
- 元のデータを復元できない
- 同じ入力からは必ず同じ出力が得られる
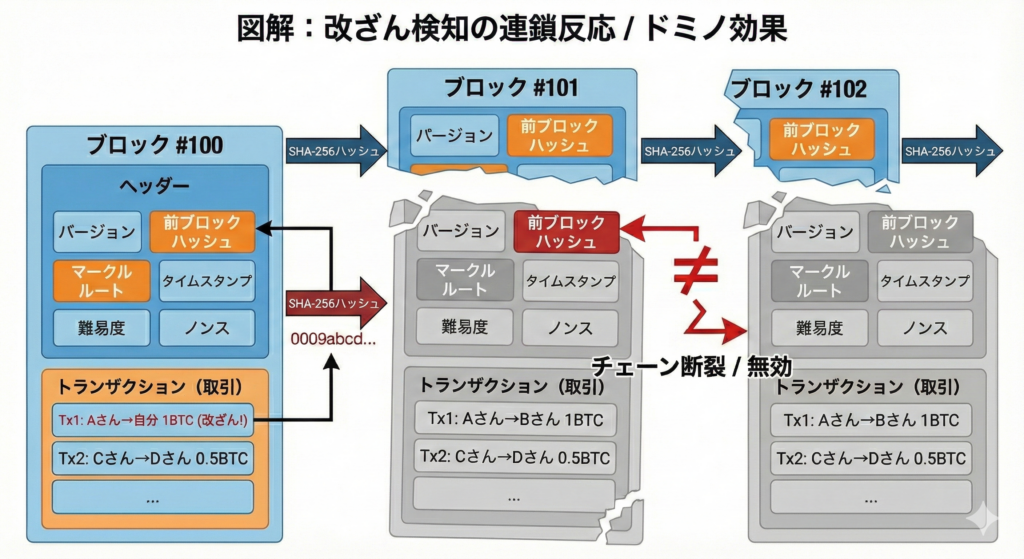
この性質により、
取引内容を少しでも書き換える
→ ハッシュが変わる
→ ブロックハッシュが変わる
→ 次のブロックとつながらなくなる
という連鎖が発生します。
改ざんは即座に検出される設計になっているのです。
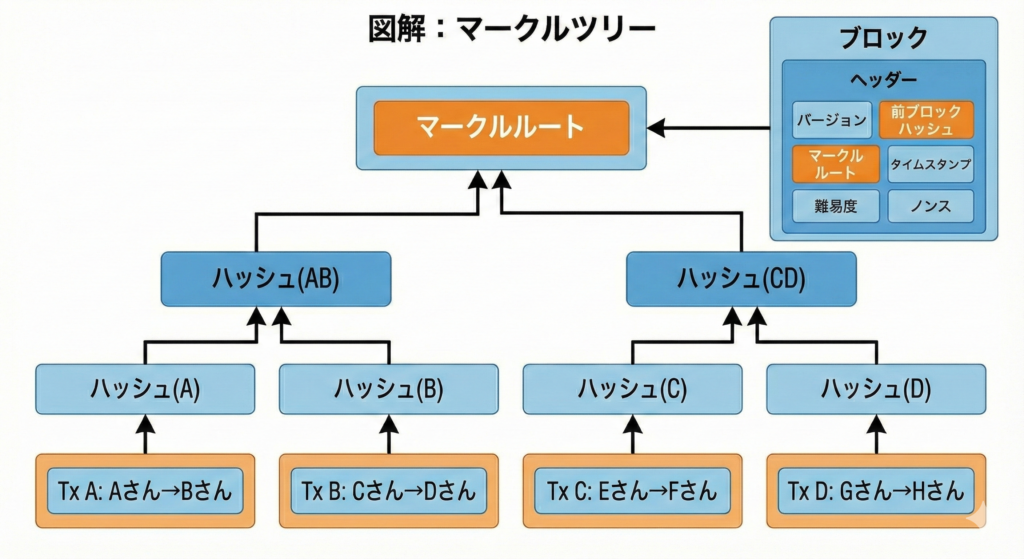
4. マークルツリー:大量の取引を1つに要約する仕組み
1つのブロックには数千件の取引が含まれます。
それらを単純に並べてハッシュ化すると非効率です。
そこで使われるのが マークルツリー です。
マークルツリーとは
- 各取引をハッシュ(葉)
- 2つずつ結合して再ハッシュ
- 最終的に1つの マークルルート に集約
なぜ必要か?
- ブロック内の取引をコンパクトに要約できる
- 軽量ノード(SPV)が最小データで検証可能
- 取引の存在証明が高速にできる
これは「分散ネットワークでも現実的に運用する」ための
極めて実務的な設計判断です。
5. 電子署名:誰が送金したかを証明する
ビットコインでは、
「この取引を実行したのが本当に本人か?」を
電子署名で証明します。
使われている技術
- 楕円曲線暗号(secp256k1)
- 公開鍵と秘密鍵のペア
ポイント
- 秘密鍵は絶対に公開されない
- 署名は「本人が・この内容で」作成した証明
- ノードは公開鍵だけで検証できる
つまりビットコインは、
信用ではなく
数学的に検証可能な証明
によって成立しています。
6. なぜ「過去は書き換えられない」のか?
ここまでの要素をまとめると理由は明確です。
- 各ブロックは前ブロックのハッシュを含む
- ハッシュは改ざん耐性を持つ
- マークルルートが取引全体を拘束する
- 電子署名が正当な所有者を証明する
- 多数のノードが同じ検証を行う
1箇所を書き換えるには、
それ以降すべてのブロックを作り直す必要がある
これが、ビットコインが
「事実上、改ざん不可能」と言われる理由です。
まとめ:ブロック構造は思想の結晶
ビットコインのブロック構造は、
単なるデータ形式ではありません。
それは、
- 中央管理者を置かず
- 誰もが検証でき
- 信頼を数学に置き換える
という思想を、
技術として極限まで突き詰めた結果です。
次のセクションでは、
このブロック構造を支える Proof of Work の深層に踏み込みます。
以下は BTC セクション3:ブロック構造と暗号技術 に対する
大学院レベル・数式寄りの補足解説です。
ブログ本文の「補論」「技術補遺」として独立掲載できる構成にしています。
技術補遺:ブロック構造と暗号技術(数式寄り/WP貼り付け用)
1) ハッシュ関数(SHA-256)の前提
ビットコインで使うハッシュ関数は、入力の長さが可変で、出力が256bit固定の関数です。
H : {0,1}* → {0,1}^256
暗号学的ハッシュに期待する代表的性質(直感+計算量)は以下です。
- 第一原像困難性:y が与えられて H(x)=y を満たす x を見つけるのが難しい(概ね O(2^256))
- 第二原像困難性:H(x)=H(x’) を満たす別の x’ を見つけるのが難しい
- 衝突困難性:H(x)=H(x’) を満たす異なる (x, x’) を見つけるのが難しい(誕生日限界で概ね O(2^128))
ビットコインでは「ダブルSHA-256」がよく登場します。
H2(x) = SHA256(SHA256(x))
2) ブロックハッシュの定義(ブロックヘッダー80バイト)
ブロックハッシュはブロックヘッダーをダブルSHA-256した値です。
BlockHash = H2(BlockHeader)
概念的にはブロックヘッダーは次のタプルで表せます。
BlockHeader = (version, prev_block_hash, merkle_root, timestamp, target, nonce)
重要なのは、prev_block_hash(前ブロックの要約)を必ず含むこと。これが「連鎖」を作ります。
—3) マークルツリー(Merkle Tree)
ブロック内の取引集合 Tx1..TxN を、木構造で1つの値(merkle_root)へ要約します。
まず各取引の要約(リーフ)を作ります。
Hi = H2(Txi) (※実装上は txid などの形で扱われる)
次に内部ノードは「2つを連結してハッシュ」します(|| は連結)。
H(i,j) = H2( Hi || Hj )
最上位の1つが merkle_root です。
包含証明(Merkle proof)のデータ量は、葉の数を N とすると概ね log2(N) 個のハッシュで足ります。
必要ハッシュ数 ≈ O(log2 N)
単純に全取引を並べてハッシュする方式だと、特定の Tx の存在証明に O(N) のデータが必要になり、SPV(軽量)ノードに不利です。
—4) 楕円曲線暗号(secp256k1)と鍵
ビットコインの署名(従来型)は ECDSA が中心で、曲線は secp256k1 を使います(有限体上の楕円曲線)。
y^2 = x^3 + 7 (mod p)
秘密鍵 k は 1..n-1 の整数、公開鍵 K は生成点 G に対するスカラー倍です。
秘密鍵: k ∈ [1, n-1]
公開鍵: K = k * G
ここで「*」は楕円曲線上のスカラー倍(点の加算を繰り返す演算)です。
—5) ECDSA署名生成(r, s)
署名対象メッセージの要約を z とします(実際はトランザクションから作る署名ハッシュ)。
ランダムな一時鍵 k’ を選びます(ここが超重要:再利用すると秘密鍵が漏れます)。
k' ∈ [1, n-1]
R = k' * G = (xR, yR)
r = xR mod n
s = (k')^{-1} * (z + r*k) mod n
署名 = (r, s)
要点:r,s は公開されても、離散対数問題の困難性により秘密鍵 k の復元はできない、という設計です。
—6) ECDSA検証(公開鍵だけで正しさを確認)
検証者は (r, s), 公開鍵 K, z を使って次を計算します。
w = s^{-1} mod n
u1 = z * w mod n
u2 = r * w mod n
Q = u1 * G + u2 * K
そして Q の x 座標が r と一致すれば検証成功です。
検証条件: (xQ mod n) = r
7) 改ざん耐性(ハッシュ連鎖を式で見る)
ブロック i の取引が1つでも変わると、リーフ→マークルルート→ブロックハッシュへ伝播します。
Tx の改変 → H(Tx) が変化 → merkle_root が変化 → BlockHash_i が変化
次ブロックでは prev_block_hash に前ブロックのハッシュが埋め込まれているため、整合性が壊れます。
prev_block_hash_(i+1) = BlockHash_i (が成立しなくなる)
よって「過去を改ざんする」とは、そこから先のブロックを整合させるよう再計算して作り直すことを意味し、PoWがあるため現実的コストが極端に高くなります。
—8) ひとことでまとめ
- ハッシュ:改ざんが即座に露見する“結合”
- マークル:大量Txを“logオーダー”で証明可能にする要約
- 署名:秘密鍵を出さずに“所有者である”ことを証明
- 連鎖:前ブロック要約を入れることで“履歴の一貫性”を強制
